A previous post described the Doppler effect in a simplified manner as it relates to movement and sound waves. This post expands on this somewhat by providing a series of Doppler effect animated images to clarify the role of a moving object and its impact on the sound.
It has been said that a picture is worth a thousand words. That being the case, then an animated image should be worth more than a thousand words. It is for this reason that this presentation illustrates the Doppler effect using animations. The animations are provided with permission from Loo Kang Wee.
Stationary Sound Source
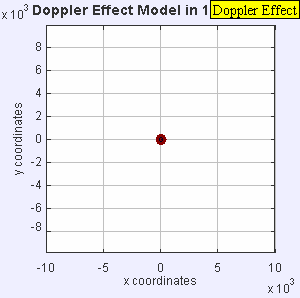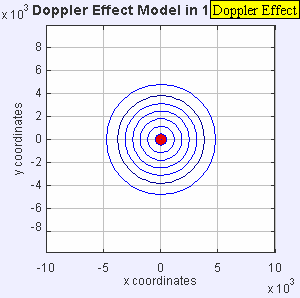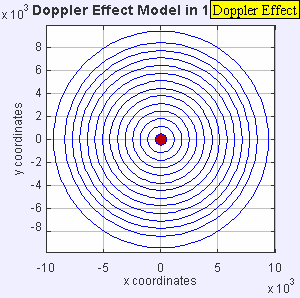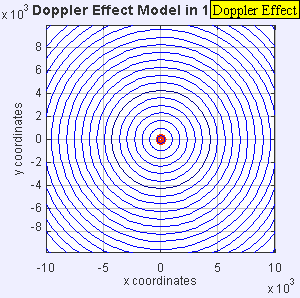
Figure 1. Animation of a sound being emitted from a stationary sound source. The sound waves propagate symmetrically away from the source at a constant speed.
A stationary sound source produces sound waves at a constant frequency. For a stationary sound source, the wave fronts propagate symmetrically away from the source at a constant speed (Figure 1), which is the speed of sound in the medium. The wavelength is the distance between the wave fronts, and all observers will hear the original signal at the same frequency. There is no Doppler effect.
Moving Sound Source
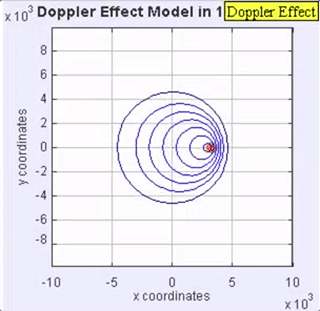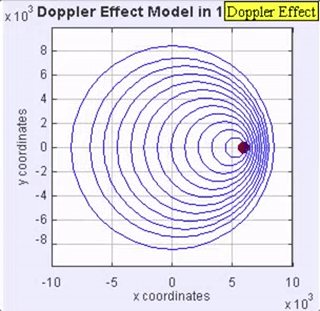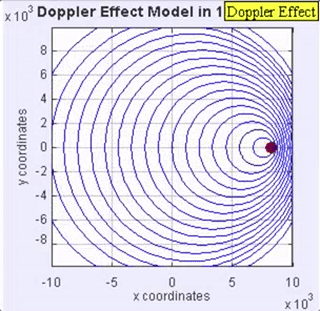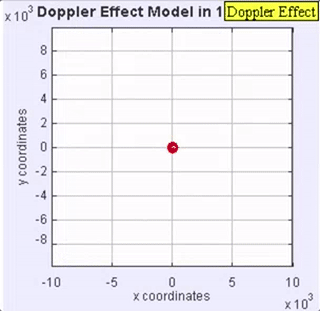
Figure 2. Doppler effect animation of a sound being emitted from a sound source moving to the right. The sound waves radiate from the source at a constant frequency. However, the wave fronts start to bunch up ahead of the moving sound source and spread out behind the moving sound source, providing the higher (bunched up) and lower (spread out) frequencies/pitches.
Figure 2 shows the same sound source radiating sound waves at a constant frequency, and in the same medium. The difference is that now the sound source is moving toward the right at a certain speed, and because of this, the center of each new wave front is now slightly displaced to the right. This results in the wave-fronts starting to bunch up on the right side (in front of the moving sound source), and then spread further apart behind the source. As a result, an observer in front of the moving source will hear a higher frequency (shorter wave lengths), and an observer behind the moving source will hear a lower frequency (longer wave lengths).
Source Moving at the Speed of Sound
When the sound source is moving rapidly at the speed of sound, the wave fronts anterior to the moving source will be bunched up at the same point (Figure 3). Because of this, an observer in front of the source will not detect any sound until the source arrives where the observer is standing (but hopefully, out of the way), and will then hear a “thump,” rather than a perceived pitch as the pressure wall passes by. The pressure front will be quite intense (a shock wave), due to all the wave fronts adding together as it passes a stationary observer.
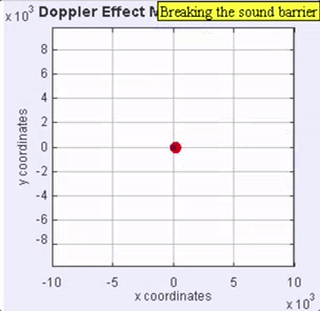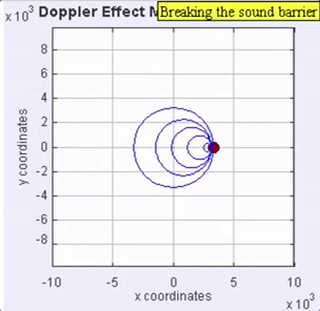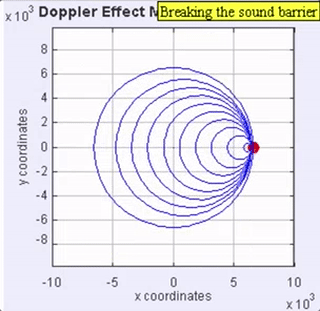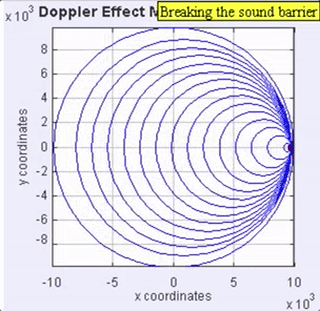
Figure 3. Animation with the sound source moving at the speed of sound (called Mach 1), in the same medium as for the other examples. No sound will be heard by an observer in front of the sound until it passes (a thump), which is then followed by the object’s sound.
Sound Source Faster Than the Speed of Sound
When the sound source surpasses the speed of sound in the medium (Mach 1 plus), it is moving faster than is the sound waves it creates. In this case, the sound source leads the advancing wave front (Figure 4), meaning that it will pass by a stationary observer before the observer hears the sound it creates. The ratio of a moving object to the speed of sound is called the Mach number, named in honor of Ernst Mach, an Austrian physicist and philosopher. So, a number of Mach 1 means that the object is moving at the speed of sound; Mach 2 at twice the speed of sound, etc.
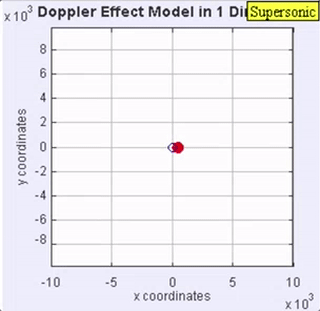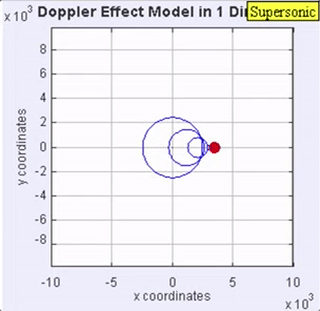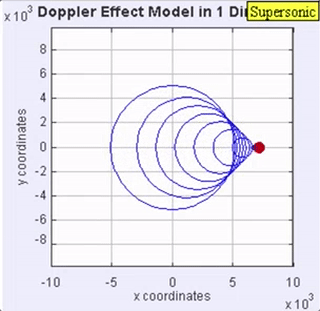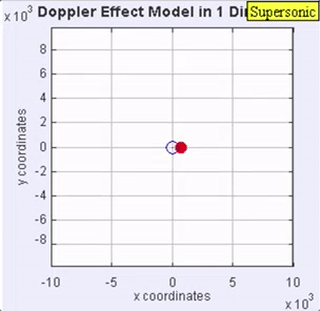
Figure 4. Animation of a supersonic sound. An observer hears no sound until some time after the sound source has passed.
Mach Cone
As you watch the animation in Figure 4, notice the clear formation of the Mach cone. The Mach cone is the shockwaves (shape of the wake of air) forming a cone that trails the aircraft (Figure 5) when it exceeds the speed of sound. The sound of the plane can be heard only if the observer is inside the Mach cone. The width of the Mach cone varies, depending on the speed of the plane as it moves through the air. The faster the plane moves, the narrower the cone becomes, and the less likely a person will hear the plane.
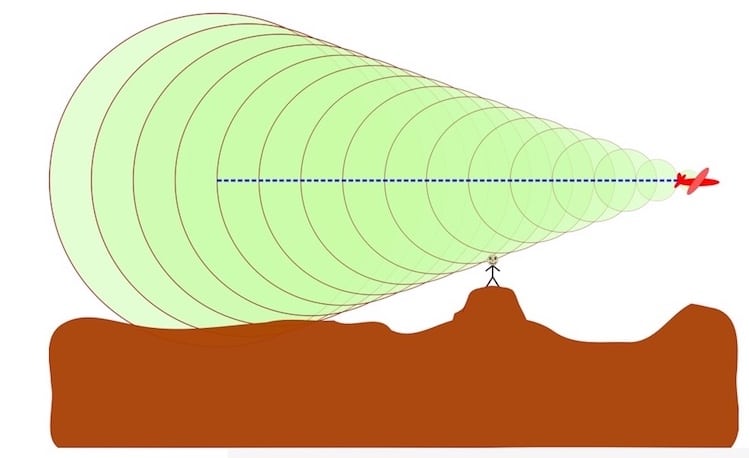
Figure 5. A sonic boom produced by an aircraft moving at M=2.92 (2.92 times the speed of sound). An observer hears the boom when the shock wave, on the edges of the cone, crosses his/her location. Picture credit: Wikipedia.

Figure 6. Mach cone visible as water vapor in the air gets trapped between pressure waves, and it briefly condenses, causing a cloud of condensed vapor to form a halo around the object. Photo made by Navy Ensign John Gay on July 7, 1999 while aboard the carrier USS Constellation, as Navy Lt. Ron Candiloro flew by.
At times, part of the Mach cone becomes visible as water vapor in the air gets trapped between pressure waves, and it briefly condenses, causing a cloud of condensed vapor to form a halo around the object (Figure 6). This halo is known as the Prandtl-Meyer expansion fan, named after their discoverers, a German engineer Ludwig Prandtl and his student, the mathematician. Figure 6 shows a photo of a F/A-18 Hornet passing through the sound barrier and forming this halo. The water vapor, density and temperature were just right to capture the moment. A smaller halo can also be seen as created by the cockpit canopy of the jet. To the observer, the halo, when seen, appears momentarily around the aircraft, and then the sonic boom is heard.
Sonic Boom
The angle of the Mach cone depends on the ratio of the source speed to the speed of sound. But, it is the intense pressure front on the Mach cone that causes the shock wave known as a sonic boom, noticed when a supersonic aircraft passes overhead. Because the shock wave advances at the speed of sound, and is built up from all the combined wave fronts, the sound heard by an observer will be quite intense. The pressure changes suddenly, through a shock, rather than in a smooth transition. A sonic boom occurs whenever an object is going Mach 1 or faster. When the sonic boom is heard, it is the leading edge of the shock wave passing over an observer on the ground.

Figure 7. Sonic boom is continually moving with the airplane, generating a boom carpet (hyperbola) on the ground following the aircraft’s flight path. A hyperbola is a symmetrical open curve formed by the intersection of a circular cone with a plane at a smaller angle with its axis than the side of the cone. The cone does not end abruptly at the back as shown in the illustration. It keeps going, but becomes less strong as it gets larger in diameter farther behind the aircraft. Modified from Paul G. Hewitt, 2006.
A common misconception is that only one boom is generated during the subsonic to supersonic transition. However, the boom is continuous along the boom carpet (a hyperbolic narrow path on the ground following the aircraft’s flight path, as if unrolling a carpet) for the entire supersonic flight (Figure 7). The width of the carpet depends on the altitude of the aircraft. Also, as the aircraft increases speed, the shock cone gets tighter around the craft, and becomes weaker to the point that at very high speeds and high altitudes, no boom is heard. Anyone standing on the ground will hear nothing until the cone reaches them, at which time they will hear an abrupt noise (sonic boom). The sudden jump in pressure occurs across a conical surface, as shown in the image. The cone moves with the airplane.
Feature image from the United States Navy