In part 1 of musical roads, we reviewed the subject of where grooves could be cut into roads such that vehicles traveling 0n them at a certain speed would generate musical notes and tunes. In Japan, South Korea, and the United States a few such musical roads exist, albeit for different reasons- in Japan and the United States as a tourist attraction (and perhaps speed control), and in South Korea to keep drivers awake.
The greater the distance between the grooves in the road, the lower the frequency that’s heard as the vehicle tires roll over them. Part 1 of this post challenged readers to calculate the exact distances between grooves necessary to generate every possible note from middle C (262 Hz) to an octave above (524 Hz), including all sharps. This was for a vehicle traveling at 100 km/h or about 62 mph. The distances would, of course, be doubled if the vehicle was traveling only 50 km/h or 31 mph.
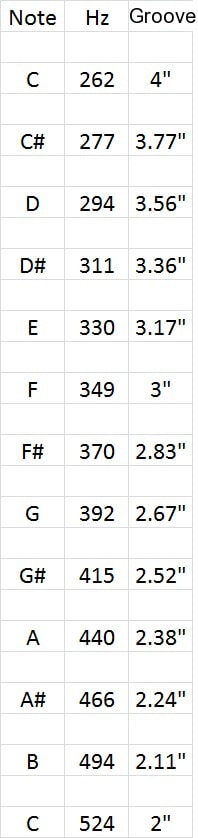 The chart to the left shows the 12 musical notes (in each octave) in column 1, the frequency of its fundamental or tonic in column 2, and the calculated groove spacing (in inches) in column 3. These were derived by dividing the necessary spacing by 1.059 from the note just below it on the piano. The figure of 1.059 is something that everyone should know and can be especially fun at parties. It’s like knowing pi to 10 decimal places- this will make you the life of the party. The figure 1.059 is the 12th root of 2. An example of its usage is as follows: If middle C is 262 Hz, then C# is 262 x 1.059 = 277 Hz. And the note above C# which is D is 277 Hz x 1.059 = 294 Hz.
The chart to the left shows the 12 musical notes (in each octave) in column 1, the frequency of its fundamental or tonic in column 2, and the calculated groove spacing (in inches) in column 3. These were derived by dividing the necessary spacing by 1.059 from the note just below it on the piano. The figure of 1.059 is something that everyone should know and can be especially fun at parties. It’s like knowing pi to 10 decimal places- this will make you the life of the party. The figure 1.059 is the 12th root of 2. An example of its usage is as follows: If middle C is 262 Hz, then C# is 262 x 1.059 = 277 Hz. And the note above C# which is D is 277 Hz x 1.059 = 294 Hz.
One thing becomes apparent from this chart. The road workers who will actually need to create these grooves (presumably with a groove machine) will need to be very accurate. A difference of even 2 tenths of an inch in groove spacing would create a note that was either a bit sharp or a bit flat.
One strategy to make this easier for the road workers who use this groove machine is to have this song played an octave or two below middle C. For an octave below middle C, the distances between grooves would double (ranging from 8” up to 4”) instead of from 4” to 2”. Another strategy would be for the posted speed limit to be 50 km/h and this in itself would allow the grooves to be placed twice as far apart compared with a 100 km/h speed limit.
Given that these two strategies are quite workable, and quite possibly these groove maker machines can be programmed, I would like to suggest that it is now time for all roads to be made musical (except in residential areas where there might be noise complaints).
I am hereby announcing MAAAAA (to be pronounced as “maaaaa” as in the sound of a lamb (as in Mary had a little lamb). This stands for Musicians And Audiologists And Acousticians Association. It is this organization that will advocate the grooving of all roads in order to bring back music, and ensure that drivers do not speed.
Consider traveling along a major highway of your choice and without warning, you start hearing Happy Birthday to You (which, by the way, is from page 262 of my favorite songbook- coincidence??). Assuming that the speed limit is 100 km/h and assuming that the song will be played in the octave below middle C, here is what the (notes and the) groove spacings (in inches) should look like…
Hap py birth day to you.
C C D C F E
8 8 7.12 8 6 6.34
Hap py birth day to you.
C C D C G F
8 8 7.12 8 5.34 6
Hap py birth day dear Hen ry.
C C C A F E D
8 8 4 4.76 6 6.34 7.12
Hap py birth day to you…
Bƅ Bƅ A F G F
4.48 4.48 4.76 6 5.34 6