Felix Baumgartner and Music

So what do music and Felix Baumgartner have in common?  Both are concerned with the speed of sound.

I just returned home from giving some talks in Zurich, Switzerland, and if you have never been to Zurich, I can tell you it is an amazingly beautiful place.  The old town is full of buildings from the 16^th century, and as in many European towns and cities, they are built along winding water ways that further enhance their appeal.  Actually, the week before I was giving some talks in San Diego which is also a beautiful city.  On the way back from San Diego I was actually flying over New Mexico at about the time that Felix Baumgartner was performing his death-defying free fall from 39 km.  He reportedly reached a speed of 1342 km/hr which is Mach 1.24 (where Mach 1 is the speed of sound). I heard a thump at about that time, but it may have only been turbulence.

Back to Switzerland!  One of the talks I was giving at the Musicians’ conference was about the physics of musical instruments.  In order to understand how the harmonic structure of a musical instrument is generated one needs to know whether the instrument functions as a quarter-wavelength or a half-wavelength instrument.  And to do the calculations one needs to know the speed of sound, but this is just foreshadowing, so forget that I even mentioned that.

Those instruments whose harmonic structure functions as a ¼-wavelength resonator are trumpets, horns, all brass instruments, and the lower register of the clarinet.  These instruments are “closed” at one end (the mouth piece or reed) and “open” at the other end (either the end of the bell or at the point of the first non-covered hole).  In contrast, stringed instruments (violin, viola, cello, bass), vocal singing, and all other wind instruments (excluding the lower register of the clarinet) function as 1/2 wavelength resonators.

The ¼-wavelength resonator formula is F = (2k-1)v/4L where L is the length of the resonator tube and v is the speed of sound.  The (2k-1) merely is a fancy way of saying that the resonances occur at odd-numbered multiples of the fundamental.  In contrast, the ½-wavelength resonator formula is F=kv/2L, which is a lot easier to write since there is no silly (2k-1) term.  Again, the L is the length of the resonating tube, v is the speed of sound, and k means that resonances occur at integer (every) multiple of the fundamental.  Half-wavelength resonators are generally better for hard of hearing people because in any given bandwidth there are roughly twice as many points of energy as with ¼-wavelength resonators.  At least that is an assumption.  This would make a great capstone topic for an AuD or graduate level audiology student- is doubling the number of harmonics in a given frequency band advantageous for listening to music for a hard of hearing person?

Turning back to that thump I heard at 37,000 feet over the New Mexico desert last week, I suppose it wasn’t Felix Baumgartner after all- he wouldn’t have been smiling so much when he landed, and probably would not have landed at all, but he was free falling at over the speed of sound.  And he was the first person to have accomplished this feat,… well maybe not, and this is where the speed of sound comes in.

In 1960, a colleague of Baumgartner who worked with him on this free fall had performed a similar feat, but from a height of “only” about 31 km.  His name is Joseph Kittinger and he is a retired colonel from the United States Air Force.  In 1960, then Captain Kittinger was involved in Project Manhigh and Project Excelsior.  Until Felix Baumgartner’s recent feat, Captain Kittinger’s 31-km dive was the world record for altitude. (It’s interesting that when a height is so great, we call it an altitude!)

It was concluded that Captain Kittinger did not break the sound barrier in 1960, but I suspect that those who had concluded this had not remembered their first year aero-acoustics class (or hearing aid or speech sciences class).  Unlike the speed of light, the speed of sound is quite variable and depends on air pressure, temperature, height, molecular content of the medium, and even latitude.

The following figure was first compiled with data from the Acoustical Society of America (and I apologize but I forgot the exact reference).  Several years ago I had modified it but had kept the essential information (and even kept the icon of Mt. Everest)

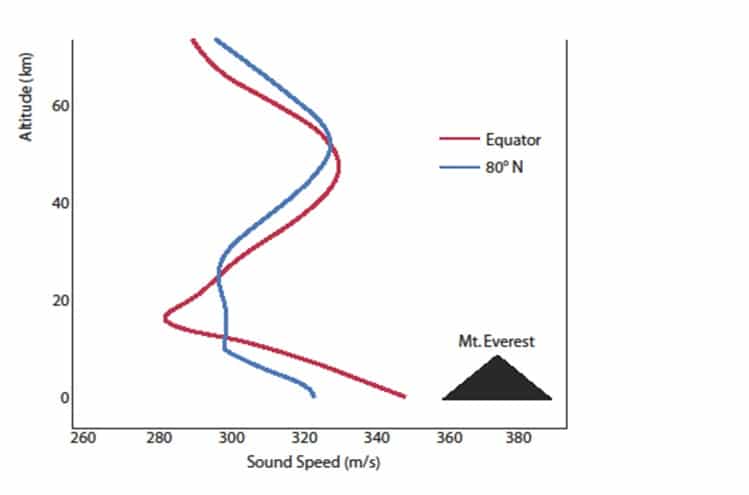
The speed of sound is dependent on many physical features such as air density, altitude, and even the latitude. At about 18 km above sea level it is at a minimum (which of course would make it easier to exceed).

At about 18 km above the earth’s surface the speed of sound is anywhere between 280 m/sec and 300 m/sec.  Sitting in a restaurant at sea level in San Diego (or in Zurich), the speed of music is probably around 335-340 m/sec, but that is not the case at an altitude of 18 km.

It is quite possible that Felix Baumgartner’s friend did indeed free fall past the sound barrier when he was 18 km above sea level in 1960.  He was going slower than Felix, but then again, the speed of sound is much slower up there.