Recently I have become involved in the development of an acoustic pillow. This is a rather interesting project and here is the story:
When people lie down to watch television on the couch, the ear against the pillow is plugged up. People lose the normal binaural summation- some benefits of two sided hearing- that they were used to experiencing. Wouldn’t it be neat if some of this “two sided hearing” could be replaced? This is where the acoustic pillow comes in. The really neat part, other than allowing people to hear better, is that the acoustic principles that are used are identical to those involved with musical instruments, hearing aid acoustics, and even vocal tract speech acoustics.
The acoustic pillow, like a trumpet, has a flare that “captures sound” and funnels it into the person’s ear that is against the pillow.
But onwards to the underlying science!
There are two acoustic phenomena that come in to play: (A) the acoustic transformer effect which has to do with the amount of flare of the horn and (B), the start frequency at which point the high frequency enhancement begins and this is related to the length (L) of the entire tube.
(A) The acoustic transformer effect:
This is related to the ratio between the cross sectional area of its neck to that of its mouth. Specifically, the “amplification factor” in decibels is given by 20 log (ratio of its cross sections). If the narrow end has a cross section of one quarter that of the wider end, then the amplification factor is 20log4 or 12 dB.
The exponential horn, regardless of shape, will enhance all higher frequencies- depending on its length-by a positive amount- depending on the ratio of the cross sectional areas at either end of the horn. This acoustic transformation allows a listener to receive a sound that has been enhanced for most of the frequency region that is necessary for optimal listening to speech and to music.
The acoustic transformer effect is seen everywhere in acoustics- that’s why certain things have a flare or horn, such as the trumpet or our mouth as we say the vowel [a] as in ‘father’- higher frequency sounds are enhanced in amplitude.
A horn is an acoustic transformer which transforms a small area diaphragm (the throat of the horn) to a large area diaphragm (the mouth of the horn). As far as the radiated power is concerned, a square or rectangular horn is equivalent to a circular one. An exponential horn has a gradually increasing cross sectional area that flares gradually much like the flare of a trumpet or other brass instrument.
So, here are two sample calculations:
- For a pillow that is 12” x 24” (or 30 cm x 60 cm) an exponential horn that flares from 1” to 10” (2.54 cm to 25.4 cm) would have the following amplification factor:
20log(25.4/2.54) = 20log10 = 20 dB
This means that a flare that starts at 1” and gradually flares to 10” would have a maximum increase of 20 dB.
- If however, the flare was smaller overall the amplification factor would be less. For example, if the flare inside the pillow was from 1” to 8” (instead of 10”) then the amplification factor would be:
20log(8) = 20 x 0.903 = 18 dB.
And here are the results for a range of “amplification factors”:
This chart shows the amplification factor (the maximum amount of gain provided by the flared horn) for each “ratio” of horn flare ranging from 1” to 2” (6 dB) to 1” to 10” (20 dB).
These data show that the maximum amount of amplification will be obtained with a larger flare ratio between the narrow part of the flare and wider part.
(B) The start frequency where amplification begins:
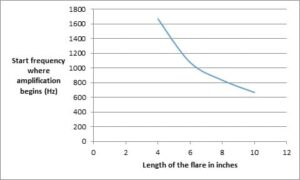
The entire length of the horn (given by L) defines the frequency range which is enhanced by the acoustic transformer effect of the flare. Specifically, all frequencies whose one half the wavelength is less than the length L are enhanced in intensity. F = v/2L where F is the frequency above which all sounds are enhanced, v is the speed of sound (approximately 33,400 cm/sec) and L is the length in cm. For example, if the flare is 25 cm long, then all frequencies will be enhanced above 668 Hz and this will increase as a function of frequency.
The length of the flare (from narrow end to wide end) defines which of the frequencies are enhanced by the pillow. The longer the flare, the lower will be the frequency start point. Bass notes will not be enhanced by the flare in the pillow, but nor will they be attenuated.
Two sample calculations are shown below:
- If the horn was 25 cm (10”) in length, then the start frequency is:
F= v/2L = 33,400 cm/sec/50 cm = 668 Hz
That is, all frequencies above 668 Hz would receive gradually increasing amplification if the horn was 25 cm or 10” long.
2. If the horn was 20 cm (8”) in length, then the start frequency is:
F= v/2L = 33,400/40 = 835 Hz.
That is, all frequencies above 835 Hz would receive gradually increasing amplification if the horn was 20 cm or 8” long.
This chart shows the start frequency, above which gradually increasing amplification can be obtained.
Conclusion… given the size limitations of a typical pillow to lay on:
Obviously for the greatest acoustical effect, the dimensions of the flare need to be the greatest. As far as the amplification factor (starting with a diameter of 1” or 2.54 cm) in the narrowest portion, the widest portion should be at least 8” (20.32 cm) with an amplification factor of 18 dB. If it can be made 10” (25.4 cm) wide at its largest dimension, then another 2 dB of maximum amplification can be obtained (with a maximum of 20 dB). Once we get below a flare of 1” to 8”, the amplification factor drops to 15.5 dB at 6”, 12 dB at 4”, and only 6 dB at 2”.
As far as the exponential horn length is considered, a 10” (25.4 cm) length would serve to amplify all sounds above 668 Hz. Most of the clarity of speech derives from frequencies above 1000 Hz so this length (10”) would be best (given that pillows are only 12” x 24” in size). Shorter lengths would yield smaller effects and would not be seen until very high frequencies.
If it came to a decision of length vs. flare, I would suggest that we try to maximize length (10”) and give up a bit on the flare ratio.
Thomas Edison and his Victrola … he really had no size limitations…
Thomas Edison knew this when he built his Victorolla. I sometimes tell my speech sciences student that Thomas was a student of mine, but I’m quite not that old.
Assuming that the Edison Victrola has a flared tube that was 1 meter in length and flared from 3 cm to 30 cm, then the amplification factor would be 20log(30/3) = 20 dB and the start frequency for amplification would be F= 33,400 / 200 = 167 Hz.
This means that the Thomas Edison Victrola amplified sounds above 167 Hz by as much as 20 dB…. Not bad for over a century ago!