Defining Power, Intensity, and Pressure
It is not uncommon to hear individuals involved with hearing aids use terminology related to sound levels incorrectly, especially power, intensity, and pressure. This, in spite of the fact that most hearing professionals had been exposed to proper use of such terms early in their careers.
This post is a very brief and simplified description of the terms of power, intensity, and pressure. Serious students, and those that understand these terms, will find this brief explanation sophomoric and of little use. However, it is the intention of this post to provide an illustrative explanation of these different terms used to describe sound to those not having that level of expertise.
Power and Intensity
Intensity – General
This is a non-specific term to describe the energy in a sound wave. It has been identified with the average rate of energy delivered to a vibrating source. It is directly related to the amplitude of a sound wave.
Energy is measured in:
- Power (intensity)
- Pressure
Power
Power refers to work done, meaning that if work has been done, energy has been expended. The unit for work is the erg (actually work in time, so, erg/second). For most work, the measurement of erg/second is too small. As a result, the power is expressed in Watts. One Watt is equal to 10 million ergs/second. Still not meaningful? How about 746 Watts equaling 1 horsepower? That still may not be meaningful, but let’s break it down anyway as follows:
- Erg – extremely small
- Erg/second – still too small
- Watts – getting closer (at least one can relate this to a light bulb)
- Horsepower – now we’re really talking power
What happens with power is that energy is radiated in all directions (Figure 1). Imagine that sound is at the center of a sphere, and as such, it travels outward from the source in all directions, it spreads over a larger area the further from the source. And, as the distance from the source increases, the intensity decreases as well. In a sphere, the area is: I=P/4πr2
What this means is that as the distance from the sound source increases by a factor of two, the intensity decreases by a factor of four.
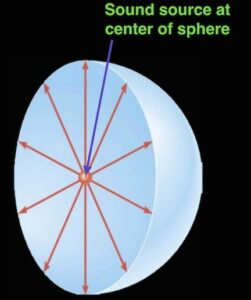
Figure 1. In power, energy is radiated in all directions, as this diagram of a sphere, with the energy source at its center, attempts to show.
To measure the power of this energy source, the sound would have to be measured around the entire circumference of the sphere at one time. This is not practical.
In electronics, the measurement of voltage calculates the same as power.
However, measuring the entire energy of a sound may not often be of interest, but instead, leads to interest in measuring that available over a small point of measurement, such as that reaching a microphone, or the eardrum (Figure 2). Measurement can be made of the energy rate transmitted along a wave through an area of 1 sq. cm at right angles to the direction of propagation. The Intensity varies with distance, and hence, the Inverse Square Law. In the case of power, this is a reduction of power by 3-dB for each doubling of the distance. (For sound pressure, the reduction is 6 dB for each doubling of distance). The comparison to power and intensity can be roughly diagrammed as in Figure 2.
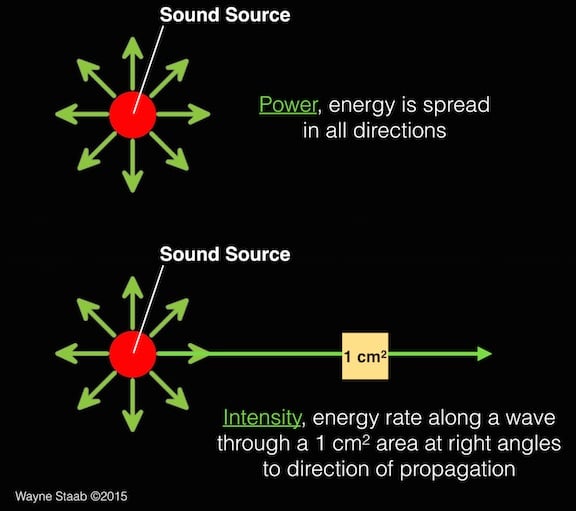
Figure 2. The lower part of this illustration shows that to measure the intensity of a sound, an area of 1 cm2 at right angles to the direction of sound propagation is used. It measures the energy rate through this area. The image at the top is used to illustrate the difference between the power of a sound and the intensity of a sound.
Pressure (P)
In hearing, we generally work with sound pressure, the method by which most sound reaches our ears via wave propagation. Air particles are moved by external forces, and the force most used is the dyne. To give one an idea, 1/30 of an ounce on the palm of the hand, provides a gravitational force of about 1000 dynes. A dyne is the amount of force necessary to move one gram one centimeter/sec/sec (Figure 3). Pressure then, is the amount of force acting over a unit surface.
In hearing, we reference pressure to the dyne. The range of human hearing is from 0.0002 dynes/cm2 to 2000 dynes/cm2. In reality, most pressures are greater than this, and so larger units are used. For example, tire pressure is measured in lbs/sq inch (10 lbs/sq inch equals pressure of about 700,000 dynes/cm2.
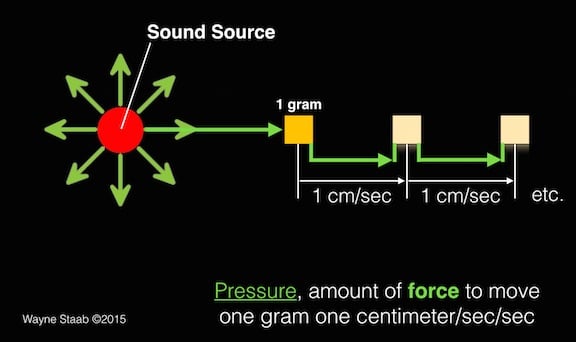
Figure 3. This illustrates the measurement of force necessary to move 1 gram (weight), one centimeter/sec/sec. Pressure is the force acting over a unit surface.