Does motion affect sound?
If you pay attention, your ears will most likely tell you the answer is “yes,” specifically in frequency. This effect is readily noticed with respect to the sound from fast-moving vehicles. When vehicles pass close to you, you will hear its sound suddenly change in pitch (frequency) just at the moment it passes by. This is an example of the well-known Doppler effect.
How a Trip Led to this Article
During a recent visit to Salzburg, Austria, and being and acting like a tourist rather than on another business trip, I got to enjoy the city in a way I had not since my first visit there in 1967. Rubber-necking, as tourists do, and taking in the architecture of an earlier era, a building, and then the sign attached to it, caught my attention – something that I had never seen on any previous trip (Figure 1). This structure is the birthplace of the physicist, Christian Doppler, who is best known for the Doppler effect. Of incidental interest, it happens to be next door to the residence of another rather famous person, Wolfgang Amadeus Mozart, who lived a generation earlier than Doppler.
Figure 1. Birthplace of Christian Doppler in Salzburg, Austria, a physicist best known for the Doppler effect. The Doppler effect explains the difference in sound perceived by an observer when there is movement between the observer and the source. As an example, how the siren of an emergency vehicle changes in pitch as it approaches and then passes by.
The Doppler Effect
The phenomenon described in the opening paragraph is an example of the Doppler effect and is visualized in Figure 2 using a firetruck and its siren as an example. The description in this post relates to sound waves, our primary area of interest, although the Doppler Effect occurs with other types of wave motion as well. Stated simply, the Doppler effect is a change in the observed frequency of a wave caused by relative motion between the source of the waves and the observer receiving them. When the waves are sound waves, the change in frequency is perceived as a change in pitch. This was first proposed in 1842 by Austrian scientist, Christian Doppler.
This post will present a very basic overview of the Doppler effect as it relates to sound.
Doppler Effect Example
A non-moving firetruck, sounding its siren, is heard at the same frequency by observer A or observer B in Figure 2a, and is illustrated by the wave lengths reaching A or B being the same because the energy propagates equally in all directions.
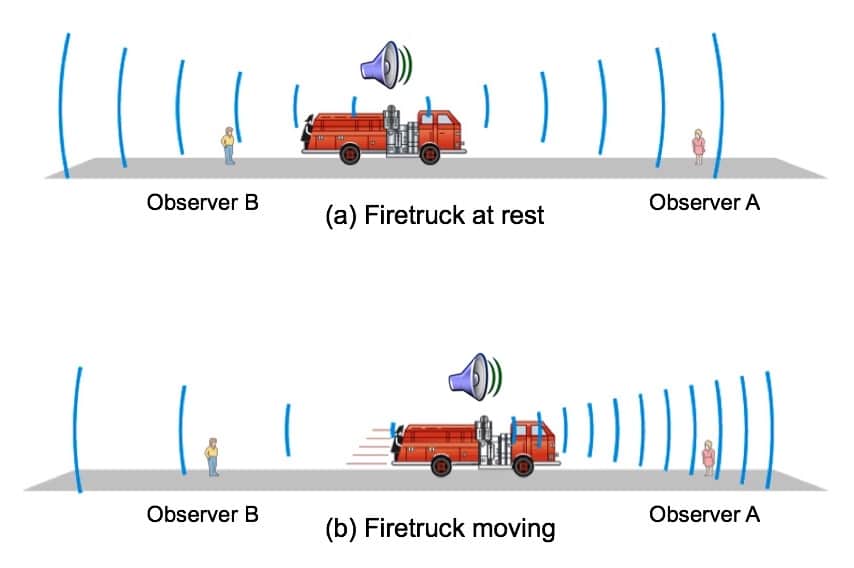
Figure 2. Simple visualization of the Doppler effect. A fast moving vehicle or sound source will demonstrate a change in frequency/pitch as it passes an observer.
However, if the firetruck is moving rapidly and approaching observer A as in 2b, that person will hear the siren at a higher frequency than normal because the sound wave crests arrive more frequently. As the firetruck passes and moves away, a drop in pitch will be heard (observer B) because the wave crests are arriving less frequently.
The Doppler effect describes the changing pitch of the siren. It is a change in the frequency experienced by an observer due to motion of either the observer or the source.
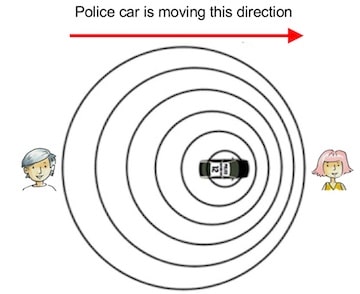
Figure 3. Illustration showing that on approaching an observer with a rapidly moving sound source, each successive wave crest is closer to its neighboring crests than if the car were not moving. The result for the woman is that the wave crests come more frequently than normal, resulting in a higher frequency, and hence higher pitch. For the man, as the sound source moves away from him, the opposite effect occurs. Wavelengths get stretched and he perceives a lowering of the frequency/pitch.
To get enough change in pitch to be actually noticeable, the relative speed between the sound source and the observer must be an appreciable fraction of the speed of sound. At normal atmospheric pressure the speed of sound is approximately 1100 feet/second. In Figure 3 imagine something that makes a noise at a definite frequency (i.e. police car siren), and moving at about 45 to 65 m/h. Imagine standing by the side of the road as the police car is approaching.
As the source of the siren sound comes toward you (woman in Figure 3), each successive wave crest is closer to its neighboring crests than if the car were not moving. For her, the wave crests come more frequently than normal, resulting in a greater frequency, and hence, a higher pitch.
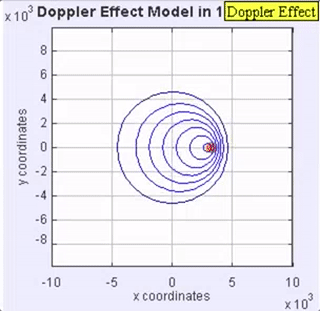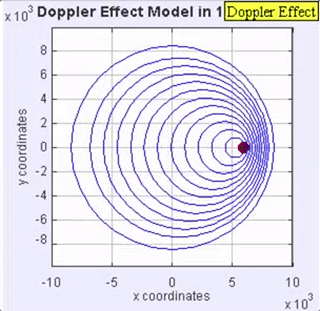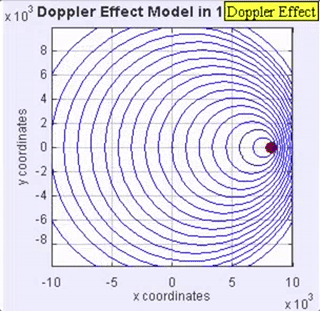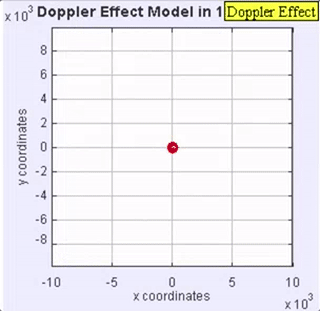
Figure 4. This animation of the wave motion associated with a sound source moving, is provided with permission from Loo Kang Wee.
For the man, as the sound source moves away from him the opposite effect occurs. He perceives a lowering of the frequency (pitch) of the sound received. For both the woman and man, the sound source is the same, but for the man, the wavelength gets stretched out because the car is moving away from him. An example of the Doppler effect with a car passing while sounding its horn can be found here. Note: The change in loudness is not the Doppler effect! It is the shift in frequency! Also, the wave speed does not change as shown in the animation in Figure 4.
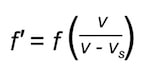The result is a simple ratio. If f is the actual frequency of the sound, v is the speed of the sound, and vs is the velocity of the source, the observed frequency f1 is equal to:
This same formula works in both directions. If vs is positive as the source is approaching, it will be negative if it is moving away (but the absolute value of vs must be less than the speed of sound, or the person in front would hear no sound at all).
The most dramatic impact of the Doppler effect occurs the instant the vehicle passes the observers location. It is during this time, which is very short, that vs changes from positive to negative, making the denominator larger. It is this sudden change of the sound source approaching to moving away (at the same speed), that produces the sudden lowering of the pitch. The greater the speed of the source, the more noticeable is the Doppler effect.
Stationary Source, Observer in Motion
A slightly different analysis occurs when the observer is moving toward or away from a stationary sound source. In this situation, the sound’s wavelength in air is the normal wavelength. The motion of the observer causes the difference in pitch because the peaks will be encountered more or less often than normal. When moving toward the stationary source, the peaks occur more often (meaning higher frequency and pitch). In the following, f is the frequency of the sound source, v is the speed of sound, v0 is the velocity of the observer. This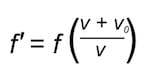 
covers both directions (moving toward and moving away from the sound source), in that v0 has a positive value when the observer is moving toward the source, and negative when moving away. Again, v0 must be restricted to absolute values less than the speed of sound.
Next week’s post will provide additional animated images of the Doppler effect.
